aeris22’s avataraeris22’s Twitter Archive—№ 92,113

    1. …in reply to @Weatherboy_fr
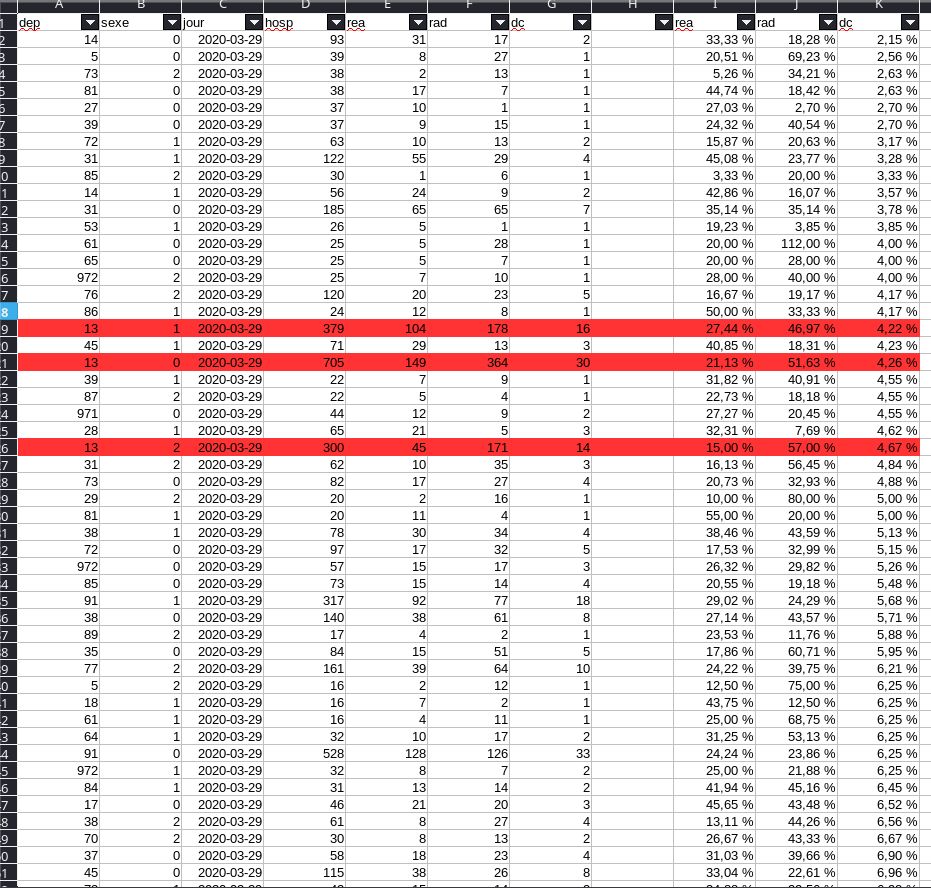
      @Weatherboy_fr @gchampeau @edasfr Chiffres officiels dispo ici : data.gouv.fr/fr/datasets/donnees-hospitalieres-relatives-a-lepidemie-de-covid-19/ Les Boûches du Rhône sont en 19ème position, dans le peloton de tête certes mais pas franchement meilleurs que d’autres.
      oh my god twitter doesn’t include alt text from images in their API
      Permalink On twitter.com Twitter logo aeris22’s avatar Mood 0
  1. …in reply to @aeris22
    @Weatherboy_fr @gchampeau @edasfr Si on filtre sur les départements avec un nombre d’hospitalisation similaires, ils sont effectivement premiers, mais pas dans des proportions folles statistiquement parlant.
    oh my god twitter doesn’t include alt text from images in their API
    On twitter.com Twitter logo aeris22’s avatar Mood 0
    1. …in reply to @aeris22
      @Weatherboy_fr @gchampeau @edasfr Je vais aussi faire un calcul plus propre, parce que ce fichier contient un biais : il donne les décès du jour et les hospitalisations du jour, le rapport n’a donc pas beaucoup de sens réel. Je vais sommer sur toute la période.
      Permalink On twitter.com Twitter logo aeris22’s avatar Mood 0
      1. …in reply to @aeris22
        @Weatherboy_fr @gchampeau @edasfr Sur les réanimations, les Bouches-du-Rhône sont dans la moyenne. Ni meilleur ni moins bon. Tout le monde tourne autour de 18-24% sur ce domaine.
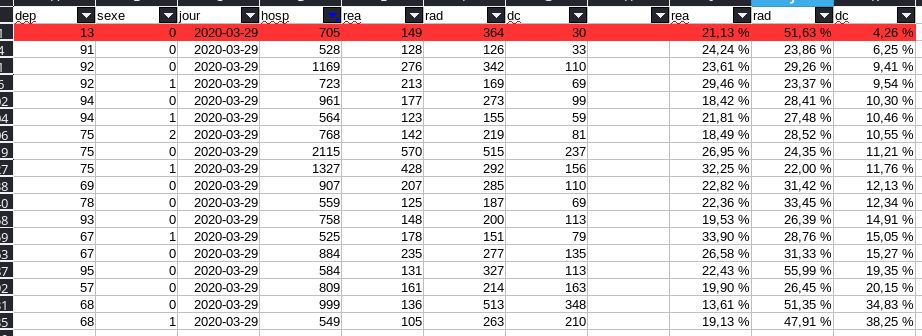
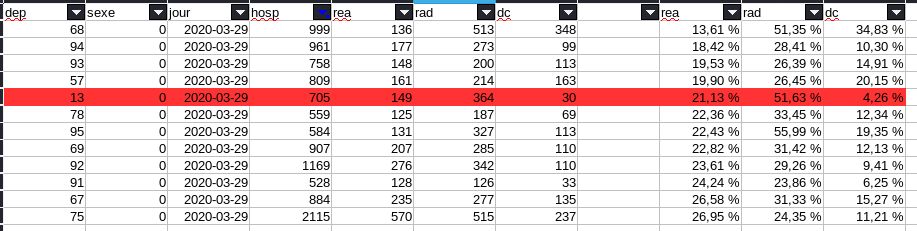
        oh my god twitter doesn’t include alt text from images in their API
        Permalink On twitter.com Twitter logo aeris22’s avatar Mood -2 🙁
        1. …in reply to @aeris22
          @Weatherboy_fr @gchampeau @edasfr Pour les décès sur des hospitalisations > 500, l’écart-type est de 8%. Donc pour une moyenne à 14.20% toute valeur entre 0 (-2% en fait 🤣) et 30% est statistiquement valide. 4.26% est donc « dans la moyenne » à 95% de chance.
          Permalink On twitter.com Twitter logo aeris22’s avatar Mood +2 🙂
          1. …in reply to @aeris22
            @Weatherboy_fr @gchampeau @edasfr Il ne s’agit donc pas d’une aberration statistique qui pourrait éventuellement donner du crédit à Raoult. Il s’agit juste des valeurs standards attendus en théorie par les statistiques… 😑
            Permalink On twitter.com Twitter logo aeris22’s avatar Mood -2 🙁
            1. …in reply to @aeris22
              @Weatherboy_fr @gchampeau @edasfr Si j’étend à tout ce qui est >100 hospitalisation, on a toujours une moyenne à 14.02% pour un écart-type de 8.53%. Donc toute valeur entre 0 et 31% est statistiquement normale avec 95% de chance.
              Permalink On twitter.com Twitter logo aeris22’s avatar Mood 0
              1. …in reply to @aeris22
                @Weatherboy_fr @gchampeau @edasfr Et c’est ça aussi la rigueur scientifique. Ne pas s’arrêter sur un chiffre qui semble bizarre ou étonnant. Mais calculer les probabilités qu’il le soit réellement. Moyenne, écart-type, 2σ voire 3σ, débiaisement des données, etc.
                Permalink On twitter.com Twitter logo aeris22’s avatar Mood -2 🙁